Model Acronym:
SWIM
Model Full Name:
Soil and Water Integrated Model
![]()
Main medium:
terrestrial
Main subject: hydrology,
biogeochemistry, vegetation
Organization level: ecosystems
Keywords: river basin, spatially
distributed, multiple sub-basins, multiple hydrotopes, three-level spatial
disaggregation, runoff, groundwater, water quality, crop yield, nutrient
cycling, nutrient transport, erosion, sediment transport, climate change, land
use change, continuous-time.
![]()
Contact:
Valentina
Krysanova
Potsdam Institute for Climate Impact Research
P.O.Box 601203, Telegrafenberg
14412 Potsdam, Germany
phone: +49-(0)331-288-2515
fax: +49-(0)331-288-2600
e-mail: valen@pik-potsdam.de
Authors:
SWIM: Valentina Krysanova & Frank Wechsung,
Potsdam Institute for Climate Impact Research
SWAT-Modules: J.G. Arnold, P.M. Allen, G.T. Bernhardt, R. Srinivasan, R.S.
Muttiah, C. Walker, P.T. Dyke, 1993, USDA & Texas A&M University
MATSALU-Modules: V. Krysanova, A. Meiner, J. Roosaare, A. Vasilyev, 1989,
Estonian Ac. Sci.
A1. Model Overview
SWIM (Soil and Water Integrated Model) is a continuous-time spatially distributed river basin
model, simulating hydrology, vegetation, erosion and nutrients (nitrogen, N,
and phosphorus, P) (Fig. 1). The
model can be applied to river basins with the area from 100 to 10000 km2,
or (after validation in representative sub-basins) to regions of that order of
magnitude. The model is described in Krysanova et al., 1998.
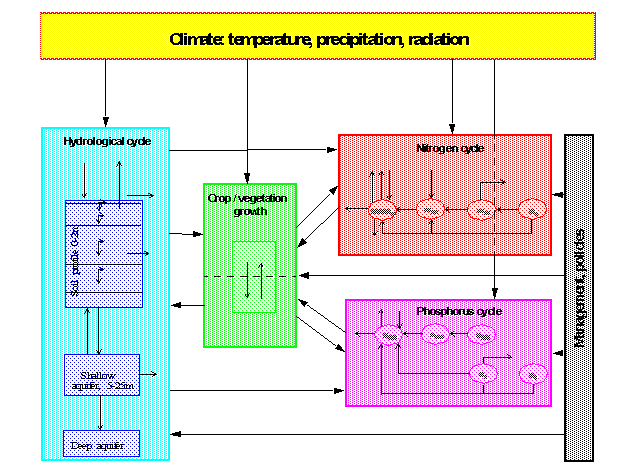
Fig. 1 Flow chart of the SWIM model, integrating hydrological processes,
crop/vegetation growth and nutrient dynamics
A three-level disaggregation scheme
(Fig. 2) plus a vertical subdivision
into a maximum of 10 soil layers are implemented in the SWIM model for
mesoscale basins: "basin - sub-basins – hydrotopes". A mesoscale
basin is firstly subdivided into sub-basins of a reasonable average area and
after that hydrotopes are delineated within every sub-basin, based on land use
and soil types. A hydrotope is a class of elementary units in the sub-basin,
which have the same land use and soil type. Climate is homogeneous at the
second level of disaggregation - for sub-basins.
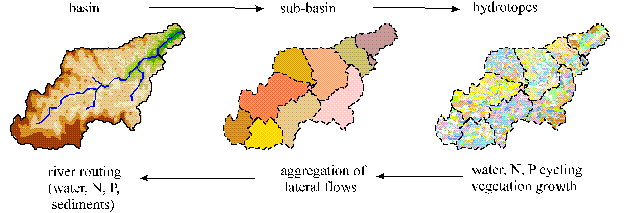
Fig 2.
Three level disaggregation scheme 'basin - sub-basins – hydrotopes‘ implemented
in SWIM
In the case of regional
applications, if the boundaries of the region do not coincide with boundaries
of any river basin, Thiessen polygons for climate stations (or grid cells of a
reasonable area) can be considered as the second level of disaggregation
instead of sub-basins.
SWIM is coupled to the Geographic
Information System GRASS (Geographic Resources Analysis Support System) to
extract spatially distributed parameters of elevation, land use, soil types,
and groundwater table. If spatially-distributed input data like Digital
Elevation Model, soil and land use maps are available in the ARC/INFO format,
they can be easily transferred to GRASS. The SWIM/GRASS interface supplies
necessary input files for the basin and sub-basins.
A2. Model history
SWIM was developed in the Potsdam
Institute for Climate Impact Research on the basis of two other models:
·
SWAT
(Arnold et al., 1993 & 1994) and
· MATSALU (Krysanova et al., 1989).
The SWAT model was developed in the
Blackland Research Center (USDA ARS, Temple, Texas) to predict the impact of
land management practices on water, sediment and agricultural chemical yields
in large complex watersheds with varying soils, land use and management
conditions. To satisfy this objective, the model is process-based, uses readily
available inputs, is computationally efficient, and enables users to study
long-term impacts. SWAT incorporates features of several ARS models and is a
direct outgrowth of the SWRRB model. Specific models that contributed
significantly to the development of SWAT were CREAMS, GLEAMS, and EPIC. The
MATSALU model developed in Estonia on the basis of CREAMS has the similar
structure as SWAT.
The model SWIM was developed with an
intention to incorporate the best features of both SWAT and MATSALU and to be
transferable to other basins in Europe. During the last three years SWIM was
extensively tested and validated in a number of mesoscale basins in Germany
(mainly belonging to the Elbe river drainage area) regarding different
processes – hydrological, vegetation, nutrients and erosion. Though still SWIM
has many common modules with SWAT, there are certain essential differences,
like the three-level spatial disaggregation scheme implemented in SWIM, a new
water routing routine based on the Muskingum method, and a new method for the
adjustment of net photosynthesis and evapotranspiration to higher CO2.
Besides that, validation of SWIM with the daily time step is an advantage in
comparison with SWAT, which is usually validated only with monthly and annual
time steps.
Model structure
The SWIM model includes hydrological
processes coupled to nutrient cycles, crop/vegetation growth, and erosion.
B1. Hydrological processes
The simulated hydrological system (Fig. 3) consists of four control
volumes: the soil surface, the root zone, the shallow aquifer, and the deep
aquifer. The soil column is subdivided into several layers in accordance with
the soil database. The water balance for the soil column includes precipitation,
surface runoff, evapotranspiration, percolation and subsurface runoff. The
water balance for the shallow aquifer includes groundwater recharge, capillary
rise to the soil profile, lateral flow, and percolation to the deep aquifer.
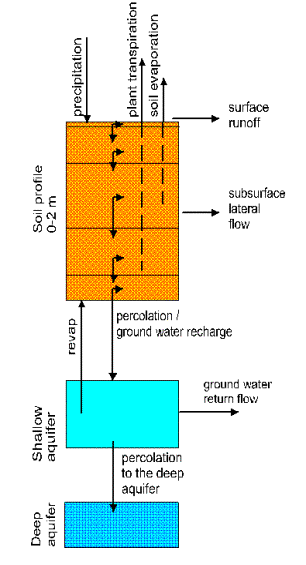
Fig. 3
Flow chart of hydrological processes in soil as implemented in SWIM
Surface runoff is estimated as a
non-linear function of precipitation and a retention coefficient, which depends
on soil water content, land use and soil type (modification of the Soil
Conservation Service (SCS) curve number method, Arnold et al., 1990). The
method was adapted to German conditions by validation in seven mesoscale river
basins of different size (all in the Elbe drainage area) and with different
climatic conditions, land use and soils. Besides, it is possible to use another
common method for runoff simulation in SWIM: to calculate runoff as a function
of precipitation and soil saturation independently of land use and soil type. Lateral
subsurface flow (or interflow) is calculated simultaneously with percolation. It
appears when the storage in any soil layer exceeds field capacity after
percolation and is especially important for soils having impermeable or less
permeable layer below several permeable ones. Potential evapotranspiration is
estimated using the method of Priestley-Taylor. Actual evaporation from soil
and actual transpiration by plants are calculated separately.
B2. The nutrient module
The nitrogen and phosphorus modules
(Fig. 4) include the following
pools: nitrate nitrogen, active and stable organic nitrogen, organic nitrogen
in the plant residue, labile phosphorus, active and stable mineral phosphorus,
organic phosphorus, and phosphorus in the plant residue, and the flows:
mineralisation, fertilization, plant uptake, lateral flows with surface and
subsurface runoff, leaching into ground water, loss with erosion,
sorption/desorption of P, and denitrification for N. Regarding the lateral
transport, the runoff and leaching are more important for nitrogen than for
phosphorus. The latter is mainly transported with erosion.
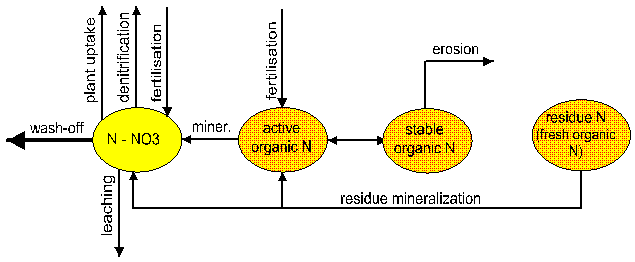
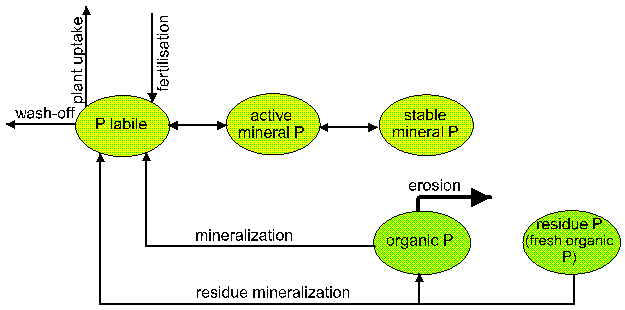
Fig 4
Nitrogen and phosphorus flow charts as implemented in SWIM
Amounts of nitrogen contained in
direct runoff, lateral subsurface flow, and leaching from soil profile are
estimated as the products of the volume of water and the average daily
concentration. Organic N transport by sediments and sediment transport of P are
simulated with a ‚loading function‘ of J. Williams (Arnold et al., 1994) from
the sediment yield, concentration of P or organic N in the top soil layer, and
the enrichment ratio. The latter is logarithmically related to sediment
concentration.
A robust approach was suggested for
modelling nutrient dynamics in mesoscale basins (Krysanova et al., 1998) and it
was applied for modelling nitrogen dynamics in the Stepenitz and Zschopau
basins with SWIM. The robust approach has the following requirements:
- the
flow chart of nutrient dynamics should be as simple as possible, but
should include the main pools of nutrients and flows between them;
- the
validation procedure should be based not only on observational data in the
basin under study (usually only measured nutrient concentrations in the
basin outlet), but also on the regionally-available information about
different nutrient balance components; and
- the
results should not be interpreted as exact predictions, but more as
indicators of possible trends and qualitative differences.
For application of the robust
approach, the published regional data on nitrogen dynamics in soils and
nitrogen flows for northern Germany were collected from literature to obtain
regionally-specific ranges for the validation of simulated nitrogen balance in
different hydrotopes.
B3. Crop/vegetation growth and yield
The module representing crop and
natural vegetation is an important interface between hydrology and nutrients. A
simplified EPIC (Williams et al., 1984 & 1989) approach is included in SWIM
(as well as in SWAT) for simulating arable crops (i. e. wheat, barley, rye,
maize, potatoes) and aggregated vegetation types (i. e. 'grass', 'pasture',
'forest'), using specific parameter values for each crop/vegetation type. It is
simplified mainly in the description of phenological processes in order to
decrease the requirements on input information. This enables crop growth to be
simulated in a distributed modelling framework at the regional scale.
A number of parameters are specified
for more than 70 crop/vegetation types in the crop database attached to the
model, i.e. biomass-energy ratio, harvest index, base and optimal temperature
for plant growth, maximum leaf area index (LAI), fraction of growing season
when LAI declines, maximum root depth, potential heat units required for
maturity of crop, and some others.
Different vegetation types affect
the hydrological cycle by the cover-specific retention coefficient, which
influences runoff, and indirectly - the amount of evapotranspiration (ET),
which is simulated as a function of potential evapotranspiration and LAI. The
interaction between vegetation and nutrient supply is modelled by the plant
consumption of nutrients and using nitrogen and phosphorus stress functions,
which affect the plant growth.
Two different approaches can be used
in SWIM for the adjustment of net photosynthesis (factor ALFA): 1) an empirical approach based on adjustment of the
biomass-energy factor as suggested in EPIC and SWAT models (Arnold et al.,
1994), and 2) a new semi-mechanistic approach derived by F.Wechsung from a
mechanistic model for leaf net assimilation (Harley et al., 1992), which takes
into account the interaction between CO2 and temperature. The second
method and its application for climate change impact study with SWIM is
described in Krysanova, Wechsung et al., 1999. Additionally, a possible
reduction of potential leaf transpiration due to higher CO2 (factor BETA) derived directly from the
enhancement of photosynthesis is taken into account in combination with both
methods for the adjustment of net photosynthesis.
B4. Erosion
Sediment yield is calculated for
each sub-basin with the Modified Universal Soil Loss Equation (MUSLE, Williams
and Berndt, 1977), almost the same as in SWAT (Arnold et al., 1994). The only
difference is that the surface runoff, the soil erodibility factor K and the
crop management factor C are estimated for every hydrotope, and then averaged
for the sub-basin (weighted areal average).
To estimate the daily rainfall
energy in the absence of time-distributed rainfall, an assumption about
exponential distribution of the rainfall rate is made. This stochastic element
is included to allow realistic representation of peak runoff rates, given only
rainfall and monthly rainfall intensity. Soil erodibility factor is estimated
from the texture of the upper soil layer. The slope length and steepness factor
is estimated from the Digital Elevation Model of a basin.
Then the sediment routing model
consisting of two components operating simultaneously – deposition and
degradation in the streams – is applied. Deposition in the stream channel is
based on the fall velocity of the sediment particles. Stream power estimated as
a function of the flow rate and the water surface slope is used to predict
degradation in the reaches.
C. Model applications
The SWIM model was tested and
validated sequentially for hydrology in several basins, for nitrogen dynamics,
crop growth, and erosion as described in the following Table:
|
No. |
Basin / gauging station or Region |
Main River, sub-region (state) |
Area, km2 |
Processes validated |
Publication in |
|
1 |
Buckener Au /Innien |
Elbe, northeast of Hamburg
(Lower Sachsony) |
64 |
hydrology |
[1], [2] |
|
2 |
Dahme / Märkisch Bucholz |
Elbe, Pleistocene lowland (Brandenburg) |
535 |
hydrology |
[1], [2] |
|
3 |
Nuthe / Babelsberg |
Elbe, Pleistocene lowland (Brandenburg) |
1876 |
hydrology |
[2] |
|
4 |
Stepenitz / Wolfshagen |
Elbe, Pleistocene lowland (Brandenburg) |
574 |
hydrology, nitrogen |
[2], [4], [6] |
|
5 |
Weiße Elster / Zeitz |
Elbe, mountainous
sub-region, (Sachsony – Thüringia) |
2479 |
hydrology |
[2] |
|
6 |
Brandenburg (regional study) |
The federal state of
Brandenburg |
» 30000 |
crop growth |
[2], [5], [7], [8] |
|
7 |
Zschopau / Lichtenwalde |
Elbe, mountainous sub-region
(Sachsony) |
1504 |
hydrology, nitrogen |
[6] |
|
8 |
Mulde / Bad Düben |
Elbe, mountainous and loess
sub-regions (Sachsony) |
6171 |
hydrology, erosion |
[3], [9] |
|
9 |
Glonn / Hohenkammer |
Isar, loess sub-region,
(Bavaria) |
392 |
hydrology,
erosion |
[9] |
|
10 |
Parthe / Leipzig-Thekla |
Elbe, loess sub-region (Sachsonia) |
315 |
hydrology |
|
References on SWIM model
- Krysanova, V., D.-I.
Müller-Wohlfeil & A. Becker (1996) Integrated Modelling of Hydrology
and Water Quality in mesoscale watersheds. PIK Report No. 18, July 1996, PIK, Potsdam.
- Krysanova, V., D.I. Müller-Wohlfeil
& A. Becker (1998) Development and test of a spatially distributed
hydrological / water quality model for mesoscale watersheds. Ecological Modelling 106 (1-2),
261-289.
- Krysanova, V., Becker
& Klöcking, B. (1998) The linkage between hydrological processes and
sediment transport at the river basin scale. In W.Summer E.Klaghover,
W.Zhang (eds.) Modelling Soil Erosion, Sediment Transport and Closely
Related Hydrological Processes. IAHS
Publications no. 249, p. 13-20.
- Krysanova, V.
& A. Becker (1999) Integrated Modelling of Hydrological Processes and
Nutrient Dynamics at the River Basin Scale, Hydrobiologia 410, 131-138.
- Krysanova,V., Wechsung,
F., Becker, A., Poschenrieder W. & Gräfe J. (1999) Mesoscale
ecohydrological modelling to analyse regional effects of climate change, Environmental Modelling and Assessment 4, 259-271.
- Krysanova, V., Gerten, D., Klöcking, B., &
Becker, A. (1999) Factors affecting nitrogen export from diffuse sources:
a modelling study in the Elbe basin. In: L. Heathwaite (ed.) Impact of
Land-Use Change on Nutrient Loads from Diffuse Sources, IAHS Publications no. 257, p.
201-212.
- Krysanova,
V., F. Wechsung, A. Meiner & A. Vasilyev, 1999. Land use
change in Europe and implications for agriculture and water resources. In: Ü. Ennuste, L. Wilder (eds.) Harmonisation
with the western economics: Estonian developments and related conceptual
and methodological frameworks, Estonian Institute of Economics at Tallinn
Technical University, 361-384.
- Wechsung, F., Krysanova, V., Flechsig M. & Shaphoff,
S. (1999) May land use change reduce the water deficiency problem caused
by reduced brown coal mining in the state of Brandenburg? Landscape and Urban Ecology (in
print)
- Krysanova,
V., Williams, J., Bürger, G. & Österle, H. 1999. Linkage
between hydrological processes and sediment transport at the river basin
scale - a modelling study. UNESCO
Technical Report on Hydrological Processes and Soil Erosion
(accepted).
Other references
- Arnold, J.G., Allen,
P.M., Bernhardt, G., 1993. A comprehensive surface-groundwater flow model. J. Hydrology, 142, 47-69.
- Arnold, J.G.,
Williams, J.R., Srinivasan, R., King, K.W., Griggs, R.H., 1994. SWAT, Soil and Water Assessment Tool.
USDA, Agriculture Research Service, Temple, TX 76502.
- Krysanova V.,
Meiner, A., Roosaare, J., Vasilyev, A. 1989. Simulation modelling of the
coastal waters pollution from agricultural watershed. Ecoogical. Modelling 49, 7-29.
- Williams, J.R., Berndt, H.D. 1977. Sediment yield
prediction based on watershed hydrology. Trans. ASAE 20 (6), 1100-1104.
- Williams, J.R., Renard, K.G., and Dyke, P.T.,
1984. EPIC – a new model for assessing erosion’s effect on soil
productivity. Journal of Soil and
Water Conservation 38 (5): 381-383.
- Williams, J.R., Jones, C.A., Kiniry J.R., and
Spanel, D.A., 1989. The EPIC Crop Growth Model. In: The Transaction of the ASAE,
Am. Soc. Of Agric. Engineers, St. Joseph, MI, USA, 32 (2), 497-511.